Matt Chiu and Tyler Howie
Steve Reich’s Mallet Quartet (2009) has enjoyed canonical success in its genre. Its rhythmic motives, as in much of Reich’s later music, gradually morph throughout the piece. This paper presents rhythmic voice leading as a pedagogical application of beat-class analysis (Cohn 1992; Roeder 2003) to identify these transformations.
Rhythmic voice leading segments the music into formal units derived from rhythmic prototypes, helping performers mentally compartmentalize, memorize, and efficiently rehearse music. For a rhythmic prototype example, take the Atsiagbekor bell pattern—a pattern Reich frequently uses (Hartenberger 2016). Marimba 1 repeats a composite rhythm composed of two different rotations of the bell pattern. Simultaneously, Marimba 2 cycles through altered bell patterns, varied by displacing onset positions, or voices. Practicing rotations of this pattern makes much of the Mallet Quartet into pattern recognition. As such, this paper serves as a practical companion for performance of this piece and others like it.
Steve Reich’s Mallet Quartet (2009) has quickly become a staple in the percussion-ensemble repertoire. Four such ensembles—the Amadinda Quartet, NEXUS, Synergy, and Sō Percussion—co-commissioned the piece (Reich 2009). Its popularity, however, is certainly not due to its percussive accessibility; it was, after all, commissioned by four professional ensembles and the piece poses performance challenges from the start. In the first movement, performers must navigate canons, hocket, and conflicting formal cues. We seek to provide a theoretical map of the first movement of the mallet quartet using primarily our concept of rhythmic voice leading—a method for describing the relationship between rhythms. By presenting the piece’s rhythmic content as a series of related transformations connected through simple voice leading, this paper acts as a performer’s companion to aid in the learning and rehearsal processes. We will begin our analysis by providing an overview of the movement’s form before introducing the concepts of beat-classes and beat-class sets, both of which other music theorists have used to analyze Reich’s music (Cohn 1992; Roeder 2003).1 We then present the three main rhythmic motives played by the marimbas and describe relationships among them using beat-class sets. Following our analysis of the marimbas’ music, we turn to the vibes’, where we use beat-classes to help us describe formal and structural relationships between the two pairs of instruments. We then place our analysis in dialogue with the one Reich offers in the score’s notes (Reich 2009). After discussing the potential performance implications of this analytical dialogue, we offer a companion practice guide based on our analyses.
Before moving on to our formal overview, we would like to take a moment to discuss some cultural context for the primary rhythmic motives of our analysis. Like other patterns Reich enjoys, these come from the dance musics of various indigenous populations in regions including West Africa, South America and the Caribbean (Locke 1987; Toussaint 2013). Other music scholars have discussed Reich’s colonization of West African rhythms (Agawu 2003; Gopinath 2019), noting in particular how he “…takes specific patterns of African music (notably bell patterns), and subjects them to distinctly ‘un-African’ processes…” (Agawu 2020). Discussions of cultural appropriation are complicated, and we do not have the space to explore this issue in the depth it deserves. But we believe that Reich—due to many factors including gender, race, nationality, location and genre—benefitted from his use of the rhythms in ways that indigenous populations did not. We analyze Reich’s use of these multicultural patterns, focusing in particular on the effects of the “distinctly un-African” processes to which he subjects them. Where possible, we give patterns culturally appropriate names, whether based on a borrowed term or their musical function, and we encourage readers and performers to engage with and discuss the complex political power structures at play in the composition, performance and analysis of a piece like Mallet Quartet.
The tonal structure of the first movement defies traditional key schemes. These key areas, defined by their scalar collections, progress by minor-third transposition—or T3. Figure 1 shows that the movement starts in an area of 2 sharps and moves through all T3 related keys: 2# → 1b → 4b → 5#, dividing the movement into four tonal areas. If we think of the key scheme as a T3-related cycle, each new tonal area is a step closer toward the cycle’s completion. The steps continue through the attacca, and the next movement continues from where the cycle began—2#s. The first movement’s key scheme is therefore directional, and the T3 cycle harmonically divides it into four sections, two of which repeat. The rhythmic motives in the marimbas, however, present a contrasting view of the first movement’s form.
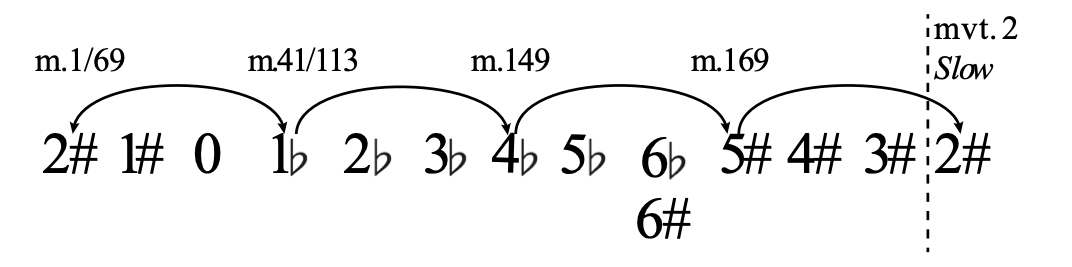
The rhythmic motives suggest a symmetrical, five-part rondo. The marimbas play two, two-bar rhythmic patterns—X and Y—which alternate to create five formal sections: XYXYX. These patterns, along with formal labels, are transcribed in Figure 2.2

Figure 3 juxtaposes the tonal and rhythmic forms of the first movement. Altogether, there are seven tonal sections (made up of four, T3-related key areas) and five rhythmic sections (made up of two alternating two-bar patterns—X and Y). We call this combination the formal aggregate. The concept of the formal aggregate can help the learning, rehearsal and performance processes. It provides multiple musical guideposts around which performers’ mental maps and ensembles’ rehearsals can be organized, and ensembles may choose to highlight certain formal divisions and obscure others in the service of a particular musical interpretation.
| Form | |||||||
|---|---|---|---|---|---|---|---|
| Measures | 1 | 41 | 69 | 113 | 149 | 169 | Mvt. II |
| Key | 2# | 1b | 2# | 1b | 4b | 5# | 2# |
| Rhythm | X | Y | X | Y | X | ||
Figure 3. Mallet Quartet, I: Formal aggregate
Having examined the form from multiple angles and created the formal aggregate, we will now turn to the rhythmic relationships used within each section. In our analysis below, we boil down the marimbas’ musical material to just three prototypical rhythms from which each unique measure-long pattern can be derived. In order to describe these relationships, we will use beat-class sets, which we will now explain.
The concept of beat classes (BCs) is rhythmically analogous to that of pitch classes. In pitch-class space, each of the twelve chromatic pitches corresponds to a number from 0–11, and octave and enharmonic equivalencies are assumed (every C is 0, C#/Db is 1, D is 2, etc.). BC space operates similarly. Each subdivisional “beat” (in our case, the eighth note) in a measure corresponds to a number. Lucky for us, the first movement of the mallet quartet is in 3/2, which means our corresponding numbers will also range from 0–11.3
Music theorists often like to represent pitch-class space as a clockface on which 12=0=C, 1=1=C#/Db. Following this convention, we visually represent our BC space in the same way. Figure 4 shows a clockface portraying both a measure of 3/2 with six eighth notes and the six pitches of a whole-tone scale, all of which land on even-numbered units; although these patterns exist in different musical spaces (pitch and rhythm), they are represented by the same mapping on a clockface.4 Note that the BC clock shows onsets, or where notes occur, rather than their durations. This means that the rhythmic pattern in Figure 4 is equivalent to a series of quarter notes.

As stated previously, we trace all of the marimbas’ rhythmic material back to three main patterns, shown in Figure 5. Before describing these rhythmic relationships, we should examine our labeling system. Each pattern has a name—bell, Tonada, and split—followed by a subscript digit (“bell0”). The subscript refers to the BC on which the pattern begins. A notable characteristic of all the three rhythms is that they each have a symmetrical property—each pattern has a unique, single axis of symmetry dividing it, and the two resulting halves can map onto each other over that axis. Because of this unique axis, each permutation of each rhythm is unique and sounds perceptually distinct from other permutations.
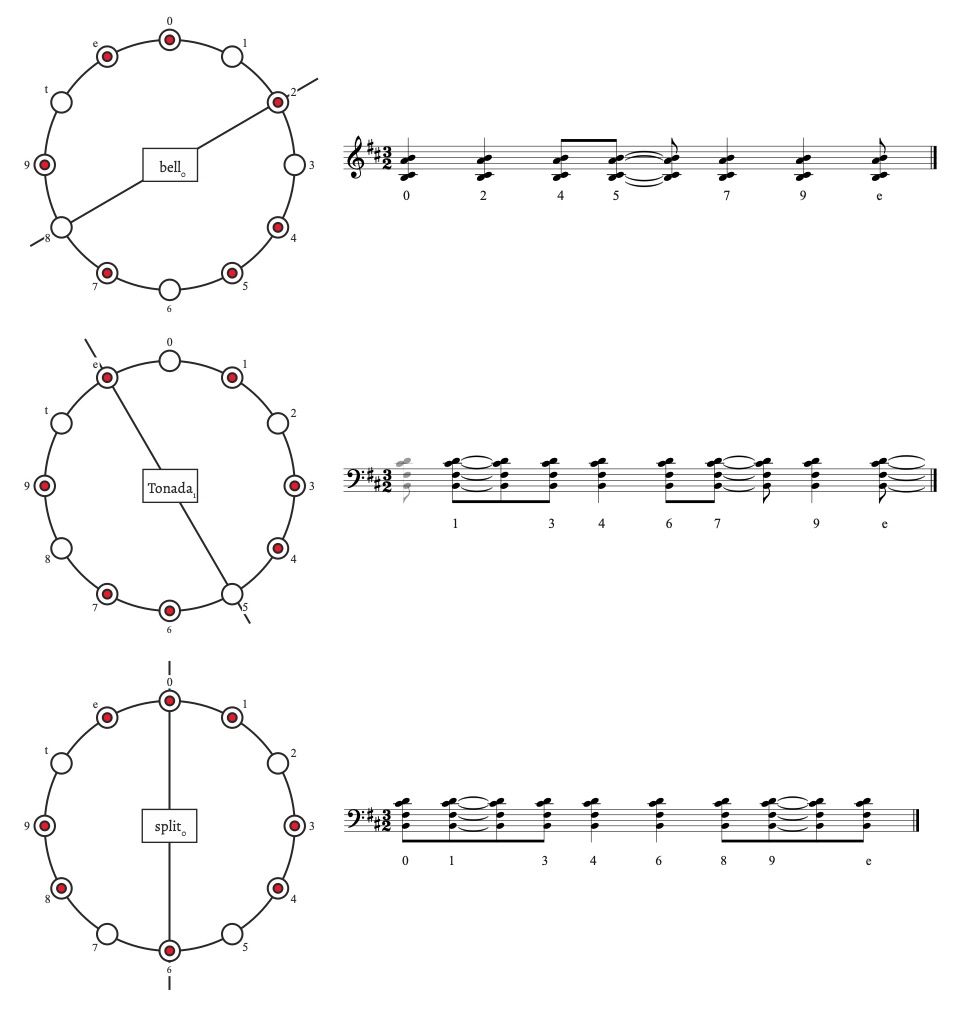
We have used culturally relevant names when possible. The “bell” pattern is found in dance musics of many cultures; Toussaint (2017) finds the pattern practiced across regions including West Africa (agbekor), South America (behavento), and the Caribbean (bembé), and more. Because it has many culturally dependent titles, we call it the “bell” pattern because of its musical function; a bell pattern in West African music, much like in the mallet quartet, is a rhythmic ostinato and guide pattern. The “Tonada” pattern is a fusion of Andalucian and African rhythms that came together in Cuba. It also appears in Bélé music in the Carribbean. We borrow the term “Tonada” from Toussaint (2005). The split pattern is the only pattern named for its relation to another—a connection we’ll explain shortly. One notable characteristic of all the rhythms in Figure 5 is that they each have a symmetrical property—each pattern has a unique, single axis of symmetry dividing it, and the two resulting halves can map onto each other over that axis. Because of this unique axis, each permutation of each rhythm is unique and sounds perceptually distinct from other permutations.
In a way, our representation of the patterns embodies the music’s effect. We combine modernist music theory and its processes with culturally relevant titles paralleling how Reich takes African materials and subjects them to un-African processes. Both groups co-opt a musical culture to serve academia’s whiteness; both present a postmodern juxtaposition of African, Cuban, South American, and Caribbean dance traditions and Western concert-hall (and academic) practices.
The bell pattern first appears in Marimba 1, m. 1. Here, it is labeled “bell0” because it starts on BC0. The bell is the most prevalent of the three main patterns, and the mallet quartet has three of its permutations: bell3, bell7, and bell8. Each of these permutations is the result of transposition. To get to bell3, transpose by bell0 by T3. Likewise, bell7 is T4 of bell3, and bell8 T1 of bell7. Figure 6 shows the transpositions of the bell pattern in notation and on BC clocks.
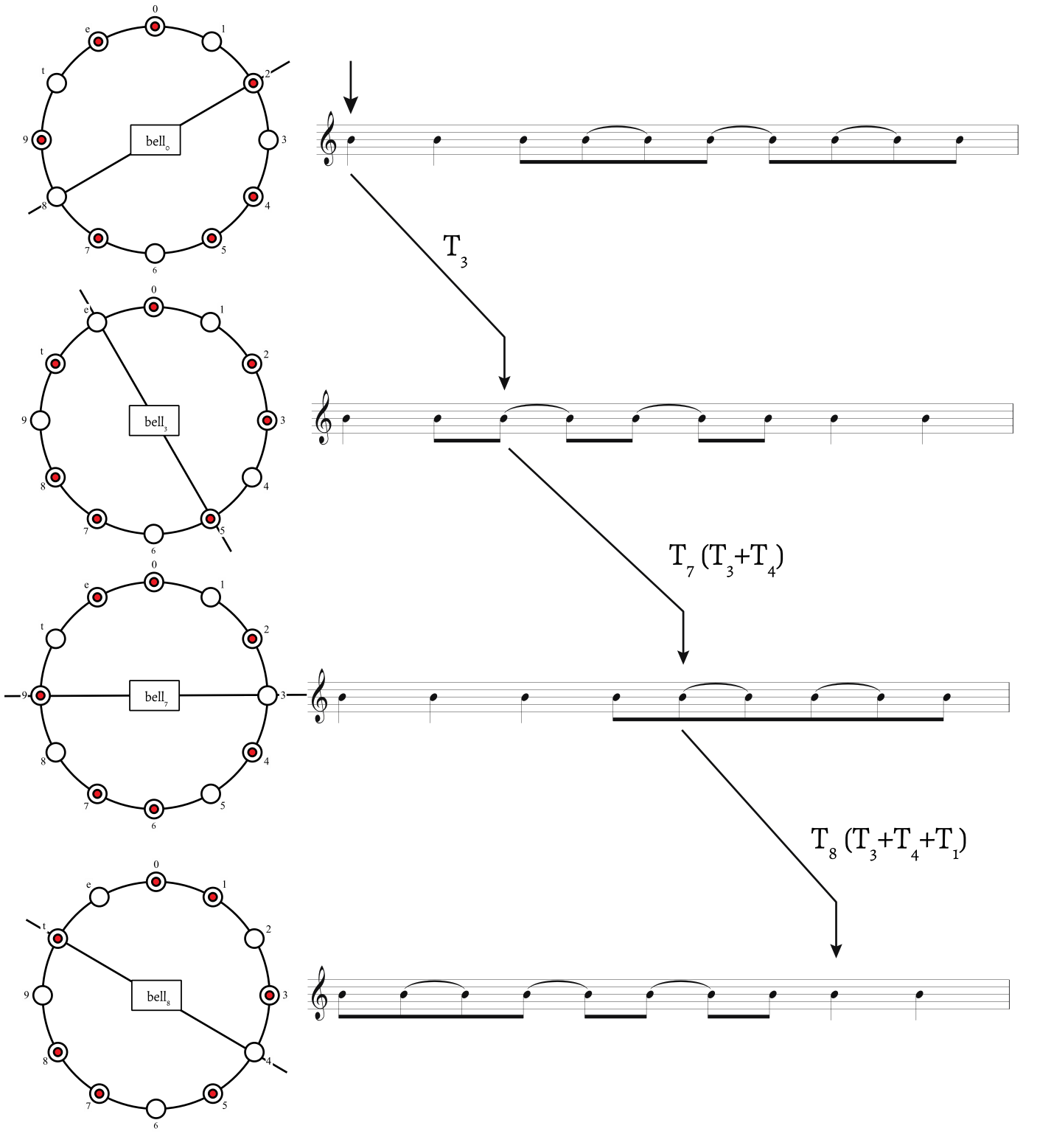
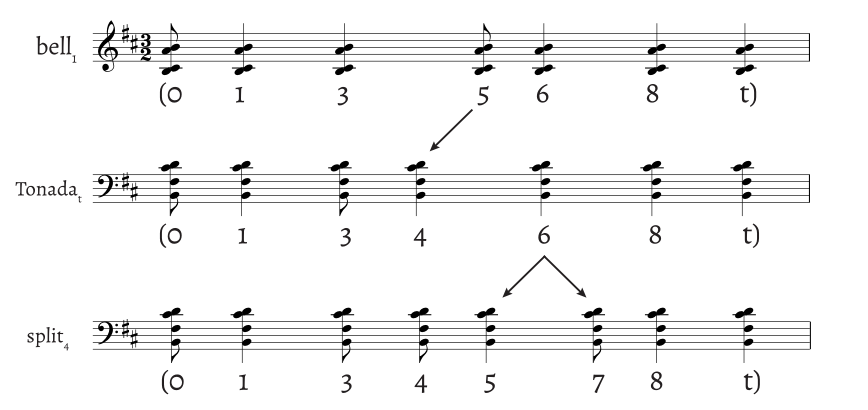
The Tonada first appears in Marimba 2, m. 1. Although it initially enters on BC0, it is labeled Tonada1 because each subsequent entry starts on BC1. Only two versions of the Tonada are present in this movement: Tonada1 and Tonada9. Much like the bell maps onto the Tonada, the Tonada maps onto the split. Figure 8 shows how each pattern can relate to one another via rhythmic voice leading. Each pattern is represented in its most compact form.5 An onset is displaced from the bell pattern results in the Tonada, and by splitting onset 6 in two, the split pattern is made; the split pattern appears in Marimba 2, m. 2 on BC0.
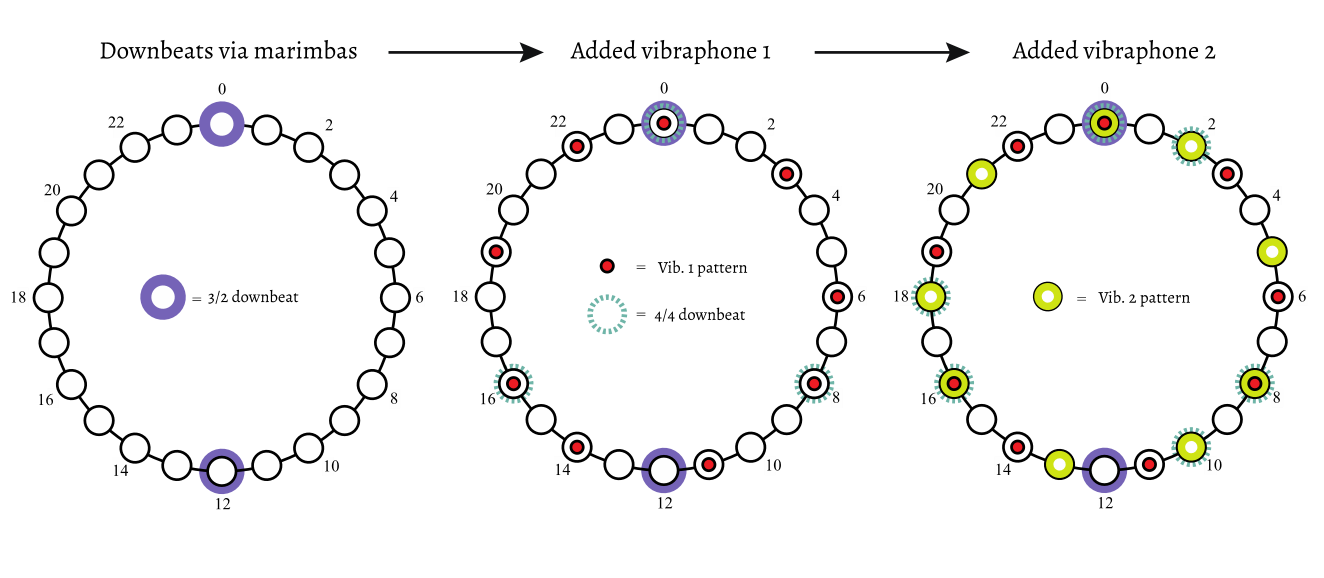
Vibe 1 enters in m. 17, playing a rhythmic pattern called the tresillo (in Cuba). It, like the bell pattern, is widely used and is known by many names. It is characterized by its 3+3+2 grouping and has been of great interest to music theorists in recent years (Toussaint 2013; London 2012; Biamonte 2013; Cohn 2016). Figure 9 shows the pattern as found in the vibraphone parts, where the 3+3+2 grouping is made clear by the highest pitch. Vibe 2 joins the texture in m. 29 and enters in canon a quarter note after Vibe 1. We can also describe the canon in BC terms: Vibe 2 enters in canon with Vibe 1 at T2.

During this canon, the marimbas continue playing their two, measure-long patterns (12+12). In the same span, the vibes play the tresillo pattern three times (8+8+8). The marimbas divide a 24-beat unit in half, and the vibes divide it in thirds, creating a two-against-three metric hemiola between the two pairs of instruments. This is further complicated when one takes into account that the vibes are in canon at T2 and the marimbas are in a repeating two-bar canon (shown in Figure 10).
As we have shown, there are many ways of structurally partitioning Mallet Quartet. We showed that the form is simultaneously directional (tonal) and alternating (rhythmic); we showed that the rhythm in the marimbas could be united by three prototypical patterns, and related through rhythmic voice leading and permutation; and, finally, we analyzed the conflicting metrical layers which resulted in a hemiola, further complicated by the canon. Reich describes the movement as two sets of canons: one in the vibes and one in the marimbas. While we did recognize the canon in the vibes, we chose to highlight different rhythmic relationships in the marimbas that are more perceptually salient. The analysis presented here prioritizes the performers’ relationship to the music rather than the larger compositional design.
We hope our view of the rhythmic relationships in the piece will help performers and ensembles in the learning, rehearsal, and performance processes. We also hope that our concept of rhythmic voice leading will be of use to performers, educators and scholars, and we encourage its alteration and application to other musical styles. As we have suggested over the course of this paper, neither analytical tools nor compositional processes are politically neutral. Our modernist music theory works well for analyzing the distinctly un-African processes Reich uses, but that does not make it universally appropriate. Notation, be it in BC sets, staff notation, or form charts, inherently prescribes communicative codes which require a specific knowledge to make meaningful, and as a result, can implicitly and/or explicitly reinforce a particular ideology. By extracting rhythms from Reich’s piece and ascribing names to the patterns from non-Western cultures, we have similarly divorced them from their experiential and cultural origins. While we hope our theory might be of use, we encourage further critical reflection on how analytical methodologies might frame, distort, or organize music.
Agawu, Kofi. 2003. Representing African Music: Postcolonial Notes, Queries, Positions. NY and London: Routledge.
———. 2020. “Rethinking Ligeti’s and Reich’s African Affiliations.” Guest lecture, AGEMS colloquium series at the University of Texas at Austin, Austin, November 10, 2020.
Biamonte, Nicole. 2014. “Formal Functions of Metric Dissonance in Rock Music.” Music Theory Online 20, no. 2.
Cohn, Richard. 1992. “Transpositional Combination of Beat-Class Sets in Steve Reich’s Phase-Shifting Music.” Perspectives of New Music 30, no. 2: 146–177.
———. 2016. “A Platonic Model of Funky Rhythms.” Music Theory Online 22, no. 2.
Gopinath, Sumanth S., and Pwyll ap Siôn. 2020. Rethinking Reich. New York, NY: Oxford University Press.
Hartenberger, Russell. 2016. Performance Practice in the Music of Steve Reich. Cambridge: Cambridge University Press.
Locke, David. 1987. Drum Gahu: The Rhythms of West African Drumming. White Cliffs Media Company.
London, Justin. 2012. Hearing in Time: Psychological Aspects of Musical Meter. New York, NY: Oxford University Press.
Reich, Steve. 2009. Mallet Quartet. NY: Boosey and Hawkes.
Roeder, John. 2003. “Beat-Class Modulation in Steve Reich’s Music.” Music Theory Spectrum 25, no. 2: 275–304.
Roig-Francolí, Miguel A,. 2008. Understanding Post-Tonal Music. Boston: McGraw-Hill.
Toussaint, Godfried. 2005. “The Euclidean Algorithm Generates Traditional Musical Rhythms.” In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science. Banff: 47–56.
———. 2013. The Geometry of Musical Rhythm: What Makes a Rhythm Good? CRC Press.
Chiu, Matt and Tyler Howie. “A Companion to Mallet Quartet: Rhythmic Voice Leading Prototypes“, DRUMMINGat50, https://drummingat50.com/2020/11/19/a-companion-to-mallet-quartet-rhythmic-voice-leading-prototypes.